cséderhúzó

Milyen volt, ami nem létezett?

Published Jan 31, 2023 Updated Jan 31, 2023 Arts and Crafts

8 min

CREATIVE ROOM

cséderhúzó

Homepage

Love

Solidarity

Wow

0 comments

581 readings

reactions

You cannot read any more publications this month without being logged in.

To enjoy unlimited access and take full advantage of new features, log in or create an account by clicking below. It's free! Log in

Milyen volt, ami nem létezett?

Lilla Czigány

Contribute

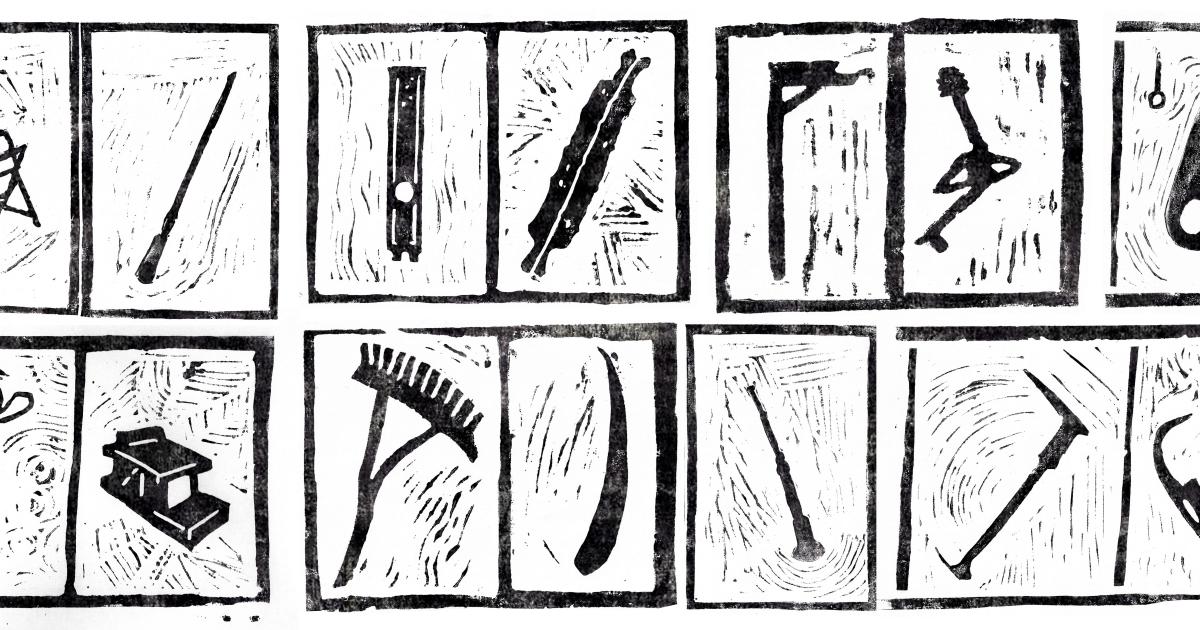
Valóban nem létezik, ami csak a gondolatainkban él? Mitől számít valódinak egy tárgy, mi ennek az igazolásnak a mércéje és biztosítéka? Hogyan dönthetjük el egy információról, hogy tényleg hiteles? Ezek a kérdések sok esetben önmaguknak is ellentmondanak, de most mégis képzeljük el, ahogy megalkotjuk egy múltbéli, nemlétező tárgy identitását, történetét, melynek a neve "cséderhúzó". Belehelyezzük a pontos időbe és térbe, konkrét funkcióval látjuk el, majd mindezek után fizikai valósággá változtatjuk a fantáziát.

De mégis miért találna ki az utókor egy múltban használatos tárgyat, főként, ha még a tárgy létezését indokló történelmi háttér, körülmények, funkciók is adott esetben kitalációk? Ténynek mondható-e egyáltalán a kitaláció? Ennek a bizonytalanságnak az alapja, hogy nincs biz